| |
 |
[ กลับหน้าหลัก ]
วางควีน 8 ตัว โดยแต่ละตัวกินกันไม่ได้
ถามเล่นๆ ว่า บนกระดานหมากรุกสากล 8x8 ช่อง
เราจะวางควีน 8 ตัว โดยแต่ละตัวจะต้องกินกันไม่ได้เลย
จะวางได้ทั้งสิ้นกี่วิธีครับ ? |
| โดย : KU41 [ 27/08/2004, 11:04:10 ] |
|
1
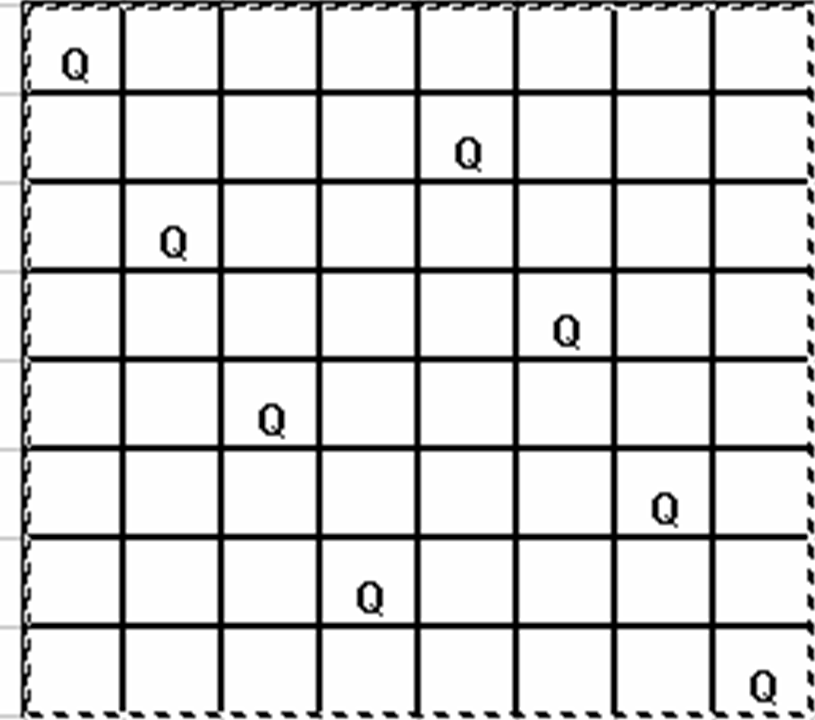
วิธีที่ 1 
|
| โดย : ม้าเจ็ก [ 27/08/2004, 11:10:21 ] |
|
2
โห คุณม้าเจ็กครับ มันหลายวิธีอยู่นา
กว่าจะลงหมด ไม่เหนื่อยแย่หรือ  |
| โดย : KU41 [ 27/08/2004, 11:23:30 ] |
|
3
จำไม่ได้แล้ว  |
| โดย : หมูหมู [ 27/08/2004, 11:27:48 ] |
|
4
ความเห็นที่ 1 ผิดแล้ว
ก็เห็นอยู่ชัดๆ ว่า Q ที่ a8 กัน h1 มันกินกันเองได้น่ะ |
| โดย : 000000001 [ 27/08/2004, 11:32:08 ] |
|
5
จริงด้วยครับ
ปล่อยไก่ตัวเบ่อเริ่มเลย
เขิลล จัง |
| โดย : ม้าเจ็ก [ 27/08/2004, 13:10:17 ] |
|
6
มื้อนี้ กินไก่กัน  |
| โดย : หมูหมู [ 27/08/2004, 13:29:03 ] |
|
7
ตัวอย่างครับ
|
| โดย : KU41 [ 27/08/2004, 14:51:51 ] |
|
8

เคยมีพี่คนหนึ่งถามอยู่.....จำได้ว่ามีประมาณ 12 วิธีค๊ะ
|
| โดย : น้องฉาว [ 27/08/2004, 20:21:19 ] |
|
9
พวกนี้นี่ เก่งๆ กันจริงๆ หนอ คิดยังไม่ทันออกเยย   |
| โดย : 000000001 [ 28/08/2004, 13:29:21 ] |
|
10
อ่ะ งั้นเอาไปอีกหนึ่งตัวอย่าง 
|
| โดย : KU41 [ 28/08/2004, 14:36:18 ] |
|
11
The eight queens problem has 92 distinct solutions, or 12 distinct solutions if symmetry operations
such as rotations and reflections of the board are taken into consideration.
ถามต่อ KU อิอิอิ
Using pieces other than queens, on an 8x8 board one can place...
32 independent knights,
or 14 bishops,
or 16 kings :-)))
How many different solutions for each of above ? อิอิอิอิ |
| โดย : 2litres [ 28/08/2004, 14:40:24 ] |
|
12

The eight queens problem has 92 distinct solutions, or 12 distinct solutions if symmetry operations
such as rotations and reflections of the board are taken into consideration.
ถามต่อ KU อิอิอิ
Using pieces other than queens, on an 8x8 board one can place...
32 independent knights,
or 14 bishops,
or 16 kings :-)))
How many different solutions for each of above ? อิอิอิอิ
|
| โดย : 2litres [ 28/08/2004, 14:40:51 ] |
|
13
คำตอบของคุณ 2litres ------------> ถูกต้องนะคร้าบบบบบบ !!!
ส่วนคำถามของคุณ 2litres ขอเอากลับไปถามคอมพิวเตอร์ก่อนครับ  |
| โดย : KU41 [ 28/08/2004, 17:51:13 ] |
|
15
ตอนแรกคิดว่า จะตอบคำถามของคุณ 2litres เมื่อเจอกันในห้อง แต่ผมเปลี่ยนใจแล้วล่ะ ขอตอบที่นี่เลยครับ

หลังจากเขียนโปรแกรมสั้น ๆ แล้ว run ด้วยคอมพิวเตอร์ที่ค่อนข้างเก่า ใช้เวลา 1 ชั่วโมง 23 นาที
ก็ได้คำตอบออกมาว่า
การวาง Bishop 14 ตัว ลงบนกระดาน 8x8 โดยไม่ให้แต่ละตัวกินกันได้นั้น ทำได้ทั้งหมด 256 วิธี
โดยมีวิธีหลัก ๆ อยู่ 36 วิธีครับ
ผิดหรือถูกอย่างไร ขอให้คุณ 2litres ตอบด้วยครับ  |
| โดย : KU41 [ 06/09/2004, 15:49:00 ] |
|
16

ขอโทษทีคับพี่เคยู พึ่งจาเห็นว่าพี่มาเขียนไว้คับผม
การวางบิชอบบนกระดาน n x n ตาโดยกินกันไม่ได้
จำนวนบิชอบที่มากที่สุด วางได้ 2n-2 ตัว
ดังนั้น บนกระดาน 8x8 ใช้บิชอบได้มากที่สุด 14 ตัวครับ
จำนวนวิธีการวางแปรผันตามขนาดตารางและเป็นไปตามอนุกรม
1,4,26,260,3368,53744,1022320,22522960,... คับผม
จำนวนวิธีที่ไม่ซ้ำกัน คิดได้จากสูตร...
(ซึ่งพิมพ์ลำบากในบอร์ดนี้ ฮ่าฮ่า)
คำตอบ 256 ไม่ถูกอ่ะครับ
แต่จำนวนวิธีที่ไม่ซ้ำกัน คือ 36 วิธี ----> ถูกต้อง
พี่เคยูยอดเยี่ยมจิงๆ ที่ถามๆตอบๆกันมาเป็นการบ้านเขียนโปรแกรมของผมทั้งหมดอ่ะ ผมเองยังทำไม่เสร็จเลย
ฮ่าฮ่า เอาอีกข้อมั้ยครับ ยังมีอีกข้อที่ปวดหัวที่ซู๊ด 
|
| โดย : 2litres [ 07/09/2004, 13:07:48 ] |
|
17
งั้นต้องเอาโปรแกรมผมไปดูแล้วล่ะ เพราะทำออกมาได้ 256 วิธีเอง
คำตอบที่ถูกเท่าไหร่ครับ  |
| โดย : KU41 [ 07/09/2004, 15:23:57 ] |
|
18
ผมเจอหน้า web pages ที่คุณ 2litres อ่านแล้วครับ  |
| โดย : KU41 [ 07/09/2004, 15:43:30 ] |
|
19
ถึงคุณ 2litres ครับ
web site หน้าที่เราได้เข้าไปอ่านและหาข้อมูลกันนั้น อ้างข้อมูลจากหนังสือ Mathematische Unterhaltungen
und Spiele ของ Wilhelm Ahrens พิมพ์โดย B.G. Teubner ที่เมือง Leipzig ประเทศเยอรมนี ปี ค.ศ. 1901 ว่า
การวางบิชอฟ 14 ตัว บนกระดาน 8x8 ทำได้ทั้งหมด 260 วิธี โดยมีวิธีหลักอยู่ 36 วิธี (หรืออาจจะพูดได้ว่า
แบ่งเป็น 36 กลุ่ม)
มีข้อสังเกตอย่างหนึ่งคือ หนังสือเล่มนั้นเก่ามาก
เป็นสมัยที่ยังไม่มีคอมพิวเตอร์ให้ใช้ช่วยตรวจความถูกต้องของการคำนวณ
โปรแกรมของผมสรุปออกมาว่า ทำได้ทั้งสิ้น 256 วิธี โดยมีวิธีหลักอยู่ 36 วิธีเช่นกัน
ผมไม่แน่ใจว่าคำตอบของใครถูกกันแน่ จึงได้เอาวิธีหลัก 36 วิธี มาทำการ 1. หมุน 90 องศา, 2. หมุน 180
องศา, 3. หมุน 270 องศา, 4. พลิกกระดาน ซ้าย-ขวา, 5. พลิกกระดาน บน-ล่าง, 6. พลิกกระดานรอบเส้นทแยงมุม
a1-h8, ึ7. พลิกกระดานรอบเส้นทแยงมุม a8-h1 (รวม 7 วิธีการ)
ซึ่งถ้าคิดแบบง่ายๆ จะเห็นว่าแต่ละวิธีการหลัก จะทำให้เกิดรูปเพิ่มมาอีก 7 วิธี ----------->
นั่นคือวิธีรวมทั้งหมด = 36 x 8 = 288 วิธี
แต่ที่วิธีจริงๆทั้งหมดมีจำนวนน้อยกว่า 288 วิธี เพราะว่า มีการซ้ำภาพกันเองขึ้นมาด้วย
ผมได้เช็คด้วยตัวเองแล้ว ขอสรุปว่าจำนวนวิธีทั้งหมด = 256 วิธีครับ ไม่ใช่ 260
วิธีตามที่หนังสือของเยอรมันเขียนไว้
เอาไว้คุณ 2litres เขียนโปรแกรมของตัวเองเสร็จแล้ว ก็ลอง run ดูครับ
ซึ่งก็น่าจะได้คำตอบเท่ากับของผมครับ  |
| โดย : KU41 [ 09/09/2004, 12:57:05 ] |
|
20
อิอิ แหม พี่เคยู อย่าไปถามหาสองลิตรกลางห้องแบบนั้นสิคับ อิอิ
เรื่องคำตอบ ผมยังเชื่อตามสมการคณิตศาสตร์อยู่นะครับ
เพราะผมมีบทความวิชาการในเรื่องที่เกี่ยวกับอนุกรมและสมการนี้อยู่บ้าง
แต่ก็ไม่กล้าสรุปว่าอันไหนผิดอันไหนถูก ขอติดไว้ก่อนนะคับผม คงต้องหาอ่านละเอียดอีกครั้ง
พลิกกระดานข้ามเส้นทะแยงมุมอาจซ้ำกับหมุน180 ครับ จำนวนวิธีคงไม่ใช่คูณแปดแน่เป็นสองแปดๆแน่
อีกสามสี่เดือนผมถึงได้เขียนโปรแกรมนี้ครับ แล้วจามาบอกอีกทีละกันคับ ขอบคุณคับโพ้ม
พี่เคยู เลิกใช้โปรแกรมเถื่อนละยังคับ อิอิ |
| โดย : 2litres [ 09/09/2004, 13:19:32 ] |
|
21
กลุ่มที่ไม่ซ้ำกันจะมี 8 รูป --------> มีกลุ่มแบบนี้อยู่ 28 กลุ่ม
แต่กลุ่มที่เกิดการซ้ำกันจะเหลือแค่ 4 รูป --------> มีกลุ่มแบบนี้อยู่ 8 กลุ่มครับ
โปรแกรมที่ผมทำ ได้เก็บคำตอบไว้ทั้ง 256 วิธี และ ระบุไว้ด้วยว่าวิธีไหนบ้างที่เป็นวิธีหลัก
ผมเอาคำตอบพวกนี้ออกมาเช็คเองอีกทีครับ
ใน web site นั้น เขียนไว้แต่สมการการหาจำนวนของวิธีหลัก เท่านั้นครับ
ไม่ได้เขียนสมการการหาจำนวนของวิธีรวมทั้งหมด 
ส่วนเรื่องโปรแกรมเถื่อนนั้น เราไม่สนับสนุนครับ อิอิ เราสนับสนุนแต่โปรแกรมของแท้เท่านั้น  |
| โดย : KU41 [ 09/09/2004, 14:04:31 ] |
|
22
งงเต๊ก |
| โดย : ส้มเช้ง [ 16/12/2004, 17:04:01 ] |
|
| |
| |
E-mail: webmaster@thaibg.com |
Copyright 2002-2025@www.ThaiBG.com (Thailand), All Rights Reserved |
|
|
| |
|

