[ กลับหน้าหลัก ]

คำถามทดลอง+ทดสอบปัญญา



สมมติผมมีลูกบอลยักษ์หนึ่งลูก
ขนาดรัศมี 1 เมตร
ผมแบ่งจากจุดศูนย์กลางทรงกลมทีละ 10 องศา
ตามรูป

โดย : zen_ar218 Member [ 25/11/2006, 19:24:22 ]

1



ผมเอามีดผ่าลูกบอลยักษืตามแนวนอน ^^
ดังรูป

โดย : zen_ar218 Member   [ 25/11/2006, 19:25:15 ]

2



คำถามง่ายมากครับ
คือ ผมอยากรู้ว่าพื้นที่ผิวของแต่ละส่วนที่ถูกผ่า มีพื้นที่เท่าไร
(รูป ที่ 1 กับ 3 เขียนแค่ครึ่งเดียว เพื่อ ดูง่ายครับ)

สูตรเส้นรอบรูปวงกลม
สอง พาย อาร์
สูตรพื้นที่วงกลม
พาย อาร์ กำลังสอง
สูตรพื้นที่ผิวทรงกลม
4 พาย อาร์ กำลังสอง
สูตรปริมาตร
1/3 พาย อาร์กำลังสาม

โทดทีนะครับโพสต์อะไรแปลกๆ
แบบว่าอยากรู้ว่าโจทย์นี้
ระดับความยากมันประมาณไหน
เซียนๆ ทุกท่านช่วยกันตอบนะครับ
คนเล่นโอ ด้วยละ โชว์หน่อย อย่าให้เสียชื่อนะครับ^^ 55555

โดย : zen_ar218 Member   [ 25/11/2006, 19:33:23 ]

3

งงครับ เซน
กึ๋นผมคงไม่ถึงมั้ง คงต้องรอท่านเทวดา ซะแว้วงานนี้

โดย : Rapin_Pri Member   [ 27/11/2006, 08:55:48 ]

4

คิดให้ตายก็ไม่ออก.......โง่มาแต่เกิด
ใครรู้ช่วยหน่อย ..คริกๆ

โดย : อึ่งอวบ Member   [ 27/11/2006, 10:44:02 ]

5

integate เส้นรอบวงก็ได้ครับ

โดย : pml Member   [ 27/11/2006, 18:24:53 ]

6

คือให้หาพื้นที่ผิว
หมายถึงถ้าผมผ่าลูกบอลยักษ์ ตามรูป แล้ว
แต่ละชิ้นที่ถูกผ่าจะมีพื้นที่ผิวเท่าไรน่ะครับ
ไม่รู้คำถามโหดไปหรือเปล่านะ

อยากให้ลองออกแนวคิดกันว่าจะหายังไงก็พอครับ
ไม่ต้องคำนวณออกมาก็ได้ครับ
^^'

โดย : zen_ar218 Member   [ 29/11/2006, 17:03:26 ]

7

ถ้าไม่ใช้ calculus แล้วมันจะคิดได้รึเปล่าคราบ

ปล. ผมเกลียด cal คราบบ

โดย : เซลด้า Member   [ 30/11/2006, 04:27:08 ]

8

รายการแบบนี้ ต้อง รอ เทวดาจร แล้วล่ะ
ฤาษี นั่งทางใน ดูแล้ว มองไม่เห็นคำตอบเลยครับ
ต้องขอโทษด้วย เกินปัญญา ฤาษี จริงๆ

โดย : ฤาษีภารตะ Member   [ 30/11/2006, 09:12:22 ]

9

ไว้ผมมาเฉลยครับ
สักสองสามวัน
...
ผมไม่ได้ใช้calculusครับ
โจทย์นี้พอดี ท่านอาจารย์ที่ผมเรียนด้วย แกให้โจทย์มาทำ
ตอนทำดวงโคม
ทดสอบเรื่องLighting เพื่อหาพื้นที่ กับความสัมพันธ์ของ
ค่าความส่องสว่าง
ผมนั่งคิดอยู่ครึ่งชั่วโมง
จะว่ายากก็ยากครับ
แต่ไม่ยากมาก ลองคิดกันดู ^^'''

โดย : zen_ar218 Member   [ 30/11/2006, 09:47:45 ]

10



มาแล้วครับ พอดีหยุดเข้าเวปไปดูซีรี่ย์ญี่ปุ่นเรื่อง "ลุ้นรักนายโอตากุ" ซะหลายวัน
ไว้จะมาโพสต์เล่าให้ฟังกันครับ

โจทย์ข้อนี้ จะไม่ยากครับ ถ้าทราบถึง ผลงานที่ อาร์คิมีดิส
ภูมิใจที่สุดในชีวิตถึงขนาดสั่งให้ทายาทสลักไว้ที่ป้ายเหนือสุสานก่อนตาย นั่นก็คือ
"ทรงกระบอกปลายเปิดที่ครอบทรงกลมได้พอดี
จะมีพื้นที่ผิวของทรงกระบอกปลายเปิดนั้นเท่ากับพื้นที่ผิวของทรงกลม"

จะสังเกตว่า คุณ เซน ให้สูตรพื้นที่ผิวของทรงกลม คือ 4*Pi*รัศมียกกำลัง2 ซึ่งสูตรนี้ก็คือก็คือ
เส้นรอบวง 2*Pi*r คูณ ความสูงทรงกระบอก 2*r นั่นเอง

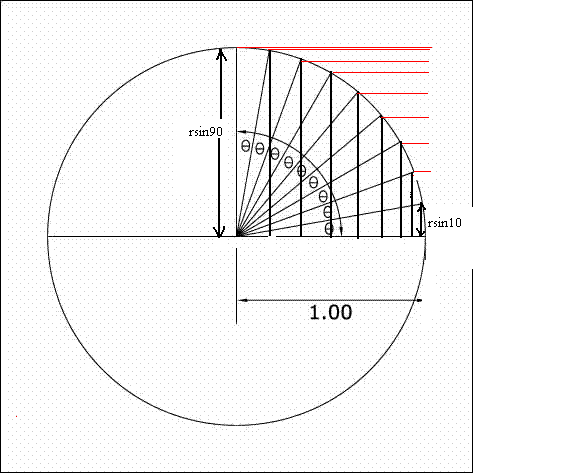
ดังนั้น เมื่อทำการเฉือนทรงกลมตามแนวนอน ตามตำแหน่งที่เกิดจากเส้นแบ่งมุม 10 องศา
ทรงกระบอกปลายเปิดที่ล้อมรอบ แต่ละชิ้นจะมีพื้นที่ผิวเท่ากับ พื้นที่ผิวชิ้นทรงกลมแต่ละชิ้น

คราวนี้เราก็ต้องมาหาความสูงของทรงกระบอกที่ครอบชิ้นส่วนแต่ละชิ้นโดยใช้สูตรทางตรีโกณมิติครับ
เราจะพิจารณาแต่ ส่วนของครึ่งทรงกลมด้านบน ซึ่งผ่าได้ 9 ชิ้น
ชิ้น 1 จะมีความสูงทรงกระบอกปลายเปิดที่ครอบ เท่ากับ r*sin10 พท.ผิว เท่ากับ
2*Pi*r*r*sin10
ชิ้น 2 จะมีความสูงทรงกระบอกปลายเปิดที่ครอบ เท่ากับ r*(sin20 - sin10) พท.ผิว เท่ากับ
2*Pi*r*r*(sin20 - sin10)
ชิ้น 3 จะมีความสูงทรงกระบอกปลายเปิดที่ครอบ เท่ากับ r*(sin30 - sin20) พท.ผิว เท่ากับ
2*Pi*r*r*(sin30 - sin10)
ทำอย่างนี้ไปเรื่อยๆ
ชิ้น 9 จะมีความสูงทรงกระบอกปลายเปิดที่ครอบ เท่ากับ r*(sin90 - sin80) พท.ผิว เท่ากับ
2*Pi*r*r*(sin90 - sin80)

เมื่อตรวจสอบคำตอบโดยนำพื้นที่ผิว ชิ้นที่ 1 ถึง ชิ้นที่ 9 บวกรวมกัน 2*Pi*r*r*sin10+2*Pi*r*r*(sin20 -
sin10)+...+2*Pi*r*r*(sin90 - sin80)
ก็จะได้ พท.ผิว รวม เท่ากับ 2*Pi*r*r*sin 90 = 2*Pi*r*r เพราะ sin 90 = 1 ซึ่งเท่ากับ
พท.ผิวของทรงกระบอกปลายเปิดที่ล้อมครึ่งทรงกลมด้านบนพอดี

ป้ายที่อยู่เหนือสุสานของอาร์คิมีดิส
ถ้าจำไม่ผิดน่าจะเป็นซิเซโรนักปราชญ์ชาวโรมันเป็นผู้บรรยายเอาไว้หลังจากเดินทางไปค้นหา
สุสานของอาร์คิมีดิสที่เสียชีวิตไปร่วม 150 ปี
"ท่ามกลางบรรดาหลุมศพคนตาย และหญ้าที่ขึ้นรกชัฎ
ข้าพจ้าได้เดินหาหลุมศพของนักคณิตศาสตร์ผู้ยิ่งใหญ่ที่สุด และ
ข้าพเจ้าก็ได้พบกับหลุมศพแห่งหนึ่ง มีป้ายไม้ ที่มีภาพ ทรงกระบอกปลายเปิดที่ล้อมรอบทรงกลมได้พอดี
ปักไว้อยู่
ผู้ที่นอนอยู่ภายในนี้จะเป็นใครเสียไม่ได้ที่จะได้นอกจากนักคณิตศาสตร์ผู้ยิ่งใหญ่ที่ข้าพเจ้ามุ่งหวังจะค
้นหา "

โดย : เทวดาจร Member   [ 30/11/2006, 11:14:44 ]

11

อย่างงี้ใช้cal คิดง่ายกว่ามั้งครับ

โดย : Guardient Member   [ 08/12/2006, 18:07:29 ]

12

หายไปนานไม่ได้มาเฉลยซักที
ติดงานอยู่ครับ
เลยไม่ได้ไปงานมีตติ้งไทยบีจีเลย
ก็มาดูเฉลยกันเลยดีกว่า

จากที่คุณเทวดาจรเฉลย
คือสิ่งที่ท่านอาร์คิมีดิสค้นพบ
นั่นคือ ทรงกระบอกที่มีความสูงเท่ากับทรงกลม(2r)
จะมีพื้นที่ผิวเท่ากับทรงกลมพอดี นั่นคือ
(2 *pi* r) * 2 r = 4 p*rยกกำลังสอง
และปริมาตรทรงกระบอกนั้นจะเป็น
2/3 เท่าของปริมาตรทรงกลม

แต่ผมไม่ได้ใช้สูตรพวกนี้หรอกครับ
แนวคิดแรกของผม คือ ลองเฉือนทรงกลมเป็นสี่เหลี่ยมและ
สามเหลี่ยมเล็กๆ ที่ขนาดเท่าๆกันดู เพื่อหาพื้นที่ แต่ปรากฎว่าไม่work
เพราะแม้จะซอยละเอียดเพียงใดก็ยังมีพื้นที่ของส่วนโค้งที่ไม่สามารถหาได้อยู่ดี ผมเลยลองวิธีใหม่ดู

โดย : zen_ar218 Member   [ 22/12/2006, 00:37:23 ]

13



ผมเริ่มจากหาพื้นที่ส่วนสีเหลืองในวงกลมภาพนี้ก่อนครับ

โดย : zen_ar218 Member   [ 22/12/2006, 00:44:06 ]

14



โทดทีครับใหญ่ไป ขออีกทีครับ

โดย : zen_ar218 Member   [ 22/12/2006, 00:45:54 ]

15



พื้นที่สีเหลืองจะหาได้ ถ้าสามารถหาพื้นที่ส่วนโค้งนี้ได้(c)
ซึ่งหาได้จากเอาพื้นที่วงกลมหาร ด้วย 36
(10 องศา)
และหักพื้นที่สามเหลี่ยมa ในรูปต่อไปออกครับ

โดย : zen_ar218 Member   [ 22/12/2006, 00:48:32 ]

16



พื้นที่สามเหลี่ยม a และ b ก็หาไม่ยาก
เรารู้ว่าเป็นสามเหลี่ยมหน้าจั่ว และรู้มุม
ก็สามารถหาพื้นที่ได้สบายๆ

ดังนั้นพื้นที่สีเหลืองจะเท่ากับ
เอาพื้นที่สามเหลี่ยมa+b +พื้นที่ส่วนโค้งc

โดย : zen_ar218 Member   [ 22/12/2006, 00:50:24 ]

17

เมื่อได้พื้นที่สีเหลืองแล้ว
คราวนี้เราจะหาพื้นที่ผิวส่วนที่ถูกผ่าก็ง่ายมากครับ
(ในที่นี้คือพื้นที่สีแดงอันล่างสุดใน คห. 2)

เพียงแค่นำพื้นที่สีเหลืองที่ท่านได้ไปคูณ ด้วย 4
ก็จะได้พื้นที่ส่วนที่ถูกผ่า ใน คห.2 แล้วครับ
ดัดแปลงมาจากสูตรพื้นที่ผิวทรงกลม
ที่จะมีพื้นที่เท่ากับ 4 เท่าของพื้นที่วงกลมไงครับ(4*pi*rกำลังสอง)

อันนี้เป็นสูตรที่ผมดัดแปลงเอง มีข้อจำกัดอยู่บ้างเหมือนกัน
แต่สำหรับโจทย์นี้สามารถใช้ได้ครับ

ทำแบบนี้กับส่วนอื่นๆอีก 8 ส่วนก็จะได้คำตอบครับ

ใกล้ปีใหม่แล้วอากาศหนาวๆ รักษาสุขภาพกันด้วยครับ
happy new year!!

โดย : zen_ar218 Member   [ 22/12/2006, 00:57:05 ]

18

โง่แคลฯ ตกเลข อิอิ ไม่รู้เรื่องอ่านแล้วงง ไม่ได้เรียนคณิตศาสตร์+ฟิสิกส์มา 8 ปี แล้วค๊าบ
(ลืมหมดอิอิ)

โดย : LimitBreak Member   [ 22/12/2006, 08:30:44 ]

19

ขออนุญาตวิเคราะห์ คห. คุณ zen น่ะครับ

1. จากความเห็น 16 แก้คำพูดที่ว่า "พท.สามเหลี่ยม a" เป็น
" พท. a " เฉยๆ ดีกว่าน่ะครับเพราะบริเวณ a ไม่ใช่สามเหลี่ยม
และก็ไม่ต้องบวก พท. ส่วนโค้ง c แล้วครับ บริเวณ a ก็คือ พท.
ทรงกลมหาร 36 ตามความหมายอยู่แล้ว

2. ฐานของ พท.สามเหลี่ยม b จะหาได้อย่างไรครับ ?

3. ตรงความเห็น 17 ของคุณ zen นี่ผมยังงงงอยู่ครับ คือ
พท.สีเหลือง เป็น 2 มิติ ไม่ใช่เหรอครับ เอา 4 คูณกลายเป็น
พท.ผิว 3 มิติ ได้อย่างไร?

กล่าวโดยสรุปง่ายๆ วิธีของผมน่าจะถูกต้องกว่า 55555

โดย : เทวดาจร Member   [ 22/12/2006, 20:38:40 ]

20

เอ่อ สมองไม่พออ่ะพี่
เอาไว้ซัก ปี 3 ปี 4 อาจจะคิดออก
เหอๆ

โดย : Natzilla Member   [ 22/12/2006, 20:59:44 ]

21

ครับ โทดทีครับ คือรูปไม่ค่อยดีเท่าไร
สามเหลี่ยมa คือรูป คห 16ที่ตัดพื้นที่ส่วนโค้งสีแดงในคห 15 ออกไปครับ
สามเหลี่ยม bก็หาง่ายครับ คือ เป็นสามเหลี่ยมหน้าจั่วเช่นกัน รู้มุม
รู้r ก็หาพื้นที่ได้

ส่วนที่ว่าคูณ 4 ได้อย่างไร เป็นสูตรลัดครับ
คือ หาพื้นที่แบนๆ ใน สองมิติ และคูณ4
***คือเป็นสูตรลัดที่ผมคิดจากพื้นที่ผิวทรงกลม ที่พื้นที่เป็นสี่เท่าของพื้นที่วงกลมครับ***
แต่ไม่สามารถใช้ได้ทุกกรณีนะครับ (ข้อนี้ใช้ได้)
ถ้าไม่แน่ใจอย่างไร ไว้ผมเฉลยตัวเลขละเอียดอีกทีครับ
ถ้าต้องการเช็ค

โดย : zen_ar218 Member   [ 23/12/2006, 00:03:29 ]

22



แค่เห็นโจทย์ก็ปวดหัวแล้วค่า...
หลังจากค้นหาจากหน่วยความจำในสมองแล้ว
ก็พบว่า...คิดไม่ออก
เห็นด้วยกับ natzilla ค่ะ ว่าไว้อีกซัก 2 ปี
รับรองคิดออกแน่ๆ

โดย : iiSonG Member   [ 23/12/2006, 02:31:06 ]

23

555 คิดออกแล้วแต่ไม่บอก มีไรเปล่า 5555

โดย : TO20 Member   [ 24/12/2006, 04:56:17 ]

24

แหะ แหะ ไม่เป็นไรหรอกครับคุณ Zen ไม่ต้องแสดงตัวเลขละเอียดหรอกครับเดี๋ยวจะเสียเวลาทำอย่างอื่นไป

โดย : เทวดาจร Member   [ 24/12/2006, 15:55:17 ]
 
  E-mail: webmaster@thaibg.com Copyright 2002-2024@www.ThaiBG.com (Thailand), All Rights Reserved  
 
  Sponsors